Brute force attack

In cryptography, a brute force attack or exhaustive key search is a strategy that can in theory be used against any encrypted data[1] by an attacker who is unable to take advantage of any weakness in an encryption system that would otherwise make his task easier. It involves systematically checking all possible keys until the correct key is found. In the worst case, this would involve traversing the entire search space.
The key length used in the encryption determines the practical feasibility of performing a brute force attack, with longer keys exponentially more difficult to crack than shorter ones. Brute force attacks can be made less effective by obfuscating the data to be encoded, something that makes it more difficult for an attacker to recognise when he has cracked the code. One of the measures of the strength of an encryption system is how long it would theoretically take an attacker to mount a successful brute force attack against it.
Contents |
Theoretical limits
The resources required for a brute force attack scale exponentially with increasing key size, not linearly. As a result, doubling the key size for an algorithm does not simply double the required number of operations, but rather squares them. Although US export regulations historically restricted key lengths to 56-bit symmetric keys (e.g. Data Encryption Standard), these restrictions are no longer in place, so modern algorithms typically use computationally stronger 128- to 256-bit keys.
| Key size in bits | Permutations |
|---|---|
| 8 | 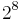 |
| 56 | 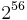 |
| 64 | 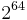 |
| 128 | 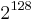 |
| 256 | 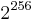 |
There is a physical argument that a 128-bit symmetric key is computationally secure against brute force attack. The so-called Von Neumann-Landauer Limit implied by the laws of physics sets a lower limit on the energy required to perform a computation of 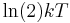 per bit erased in a computation, where T is the temperature of the computing device in kelvins, k is the Boltzmann constant, and the natural logarithm of 2 is about 0.693. No irreversible computing device can use less energy than this, even in principle.[2] Thus, in order to simply flip through the possible values for a 128-bit symmetric key (ignoring doing the actual computing to check it) would theoretically require 2128 − 1 bit flips on a convential processor. If it is assumed that the calculation occurs near room temperature (~300 K) the Von Neumann-Landauer Limit can be applied to estimate the energy required as ~1018 joules, which is equivalent to consuming 30 gigawatts of power for one year (30×109 W×365×24×3600 s = 9.46×1017 J). The full actual computation—checking each key to see if you have found a solution—would consume many times this amount.
per bit erased in a computation, where T is the temperature of the computing device in kelvins, k is the Boltzmann constant, and the natural logarithm of 2 is about 0.693. No irreversible computing device can use less energy than this, even in principle.[2] Thus, in order to simply flip through the possible values for a 128-bit symmetric key (ignoring doing the actual computing to check it) would theoretically require 2128 − 1 bit flips on a convential processor. If it is assumed that the calculation occurs near room temperature (~300 K) the Von Neumann-Landauer Limit can be applied to estimate the energy required as ~1018 joules, which is equivalent to consuming 30 gigawatts of power for one year (30×109 W×365×24×3600 s = 9.46×1017 J). The full actual computation—checking each key to see if you have found a solution—would consume many times this amount.
However, this argument assumes that the register values are changed using conventional set and clear operations which inevitably generate entropy. It has been shown that computational hardware can be designed not to encounter this theoretical obstruction (see reversible computing), though no such computers are known to have been constructed.
As commercial available successors of governmental ASICs Solution also known as Custom hardware attack, today two emerging technologies have proven their capability in the brute force attack of certain ciphers. One is modern GPU technology the other is the FPGA technology.
GPUs benefit from their availability, FPGAs from their energy efficiency per crypto operation. Both technologies try to transport the benefits of parallel processing to brute force attacks. In case of GPUs some hundreds in the case of FPGA some thousand processing units making them much better suited to cracking passwords than conventional processors. Various publications in the fields of cryptanalysis have proved the energy efficiency of today’s FPGA technology, e.g. COPACOBANA FPGA Cluster computer consumes the same energy a single PC (600W) but performs like 2500 for certain algorithms. FPGA clusters are often seen like the "Deep Crack" developed by by the Electronic Frontier Foundation as custom hardware attack. However multiple firms provide FPGA cryptanalysis solutions form single FPGA PCI Express cards like GPU cards up to fully equipped FPGA Computers. WPA and WPA2 encryption has successfully been brute-force attacked in this way by reducing the workload by a factor of 50 in case of CPUs[3][4] and some hundred in case of FPGAs.
AES permits the use of 256-bit keys. Breaking a symmetric 256-bit key by brute force requires 2128 times more computational power than a 128-bit key. A device that could check a billion billion (1018) AES keys per second would require about 3×1051 years to exhaust the 256-bit key space.
An underlying assumption of this analysis is that the complete keyspace is used to generate keys, something that relies on an effective random number generator. For example, a number of systems that were originally thought to be impossible to crack by brute force have nevertheless been cracked in this way because the key space to search through was found to be much smaller than originally thought, due to a lack of entropy in their pseudorandom number generators. These include Netscape's implementation of SSL (famously cracked by Ian Goldberg and David Wagner in 1995[5]) and a Debian edition of OpenSSL discovered in 2008 to be flawed.[6]
Hybrid attacks
Brute force attacks may be optimised through the use of a dictionary attack—humans are more likely to choose words in every day language for their passwords than completely random passwords. An attacker may therefore have a greater chance of early success by trying these combinations first.
Unbreakable codes
Certain types of encryption, by their mathematical properties, cannot be defeated by brute force. An example of this is one-time pad cryptography, where every cleartext bit has a corresponding key bit. One-time pads rely on the ability to generate a truly random sequence of key bits. A brute force attack would eventually reveal the correct decoding, but also every other possible combination of bits, and would have no way of distinguishing one from the other. A small, 100-byte, one-time-pad–encoded string subjected to a brute force attack would eventually reveal every 100-byte string possible, including the correct answer, but mostly nonsense. Of all the answers given, there is no way of knowing which is the correct one. Nevertheless, the system can be defeated if not implemented correctly, for example if one-time pads are re-used or intercepted.[7]
Countermeasures
In the case of an offline attack where the attacker has access to the encrypted material, he can try key combinations at his leisure without the risk of discovery or interference. However database and directory administrators can take countermeasures against online attacks, for example by limiting the number of attempts that a password can be tried, by introducing time delays between successive attempts and locking accounts out after unsuccessful logon attempts.[8] Website administrators may prevent a particular IP address from trying more than a predetermined number of password attempts against any account on the site.[9]
See also
- Side-channel attack
- Cryptographic key length for a fuller discussion of recommended key sizes for symmetric and asymmetric algorithms.
- TWINKLE and TWIRL
- 40-bit encryption
- Distributed.net
- MD5CRK
- Unicity distance
- RSA Factoring Challenge
- Custom hardware attack
- Dictionary attack
References
- ↑ Christof Paar, Jan Pelzl, Bart Preneel (2010). Understanding Cryptography: A Textbook for Students and Practitioners. Springer. p. 7. ISBN 3642041000. http://books.google.com/books?id=f24wFELSzkoC.
- ↑ Rolf Landauer, "Irreversibility and heat generation in the computing process," IBM Journal of Research and Development, vol. 5, pp. 183-191, 1961.
- ↑ Adrian Kingsley-Hughes (2008-10-12). "ElcomSoft uses NVIDIA GPUs to Speed up WPA/WPA2 Brute-force Attack". ZDNet. http://www.zdnet.com/blog/hardware/elcomsoft-uses-nvidia-gpus-to-speed-up-wpawpa2-brute-force-attack/2724.
- ↑ Erik Kamerling (2007-11-12). "Elcomsoft Debuts Graphics Processing Unit (GPU) Password Recovery Advancement". Symantec. http://www.symantec.com/connect/blogs/elcomsoft-debuts-graphics-processing-unit-gpu-password-recovery-advancement.
- ↑ John Viega, Matt Messier, Pravir Chandra (2002). Network Security with OpenSS. O'Reilly. pp. 18. ISBN 059600270X. http://books.google.com/?id=FBYHEBTrZUwC. Retrieved 2008-11-25.
- ↑ "Technical Cyber Security Alert TA08-137A: Debian/Ubuntu OpenSSL Random Number Generator Vulnerability". United States Computer Emergency Readiness Team. 2008-05-16. http://www.us-cert.gov/cas/techalerts/TA08-137A.html. Retrieved 2008-08-10.
- ↑ Robert Reynard (1997). Secret Code Breaker II: A Cryptanalyst's Handbook. Jacksonville, FL: Smith & Daniel Marketing. pp. 86. ISBN 1889668060. http://books.google.com/?id=3nTmBW0ONEEC&pg=PA86. Retrieved 2008-09-21.
- ↑ Mark Burnett, James C. Foster (2004). Hacking the Code: ASP.NET Web Application Security. Syngress. ISBN 1932266658. http://books.google.com/books?id=-WShG0uezvEC.
- ↑ Ivan Ristic (2010). Modsecurity Handbook. Feisty Duck. p. 136. ISBN 1907117024. http://books.google.com/books?id=HnQl5OVtOYgC.
- Leonard M. Adleman, Paul W. K. Rothemund, Sam Roweis and Erik Winfree, On Applying Molecular Computation To The Data Encryption Standard, in Proceedings of the Second Annual Meeting on DNA Based Computers, Princeton University, June 10–12, 1996.
- Cracking DES — Secrets of Encryption Research, Wiretap Politics & Chip Design by the Electronic Frontier Foundation (ISBN 1-56592-520-3).
- W. Diffie and M.E. Hellman, Exhaustive cryptanalysis of the NBS Data Encryption Standard, Computer 10 (1977), pp 74–84.
- Michael J. Wiener, "Efficient DES Key Search", presented at the rump session of Crypto 93; reprinted in Practical Cryptography for Data Internetworks, W. Stallings, editor, IEEE Computer Society Press, pp 31–79 (1996).
External links
- Brute force attacks on cryptographic keys — a survey by Richard Clayton
- DES cracking contest
- www.keylength.com: An online keylength calculator
- The COPACOBANA (Cost-Optimized Parallel COde Breaker) reconfigurable code breaker
- phrel: A Linux utility to help prevent brute force attacks on FTP, DNS and other protocols.
- WASC Threat Classification - Brute Force
|
||||||||||